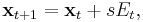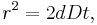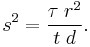Cuckoo search

Cuckoo search (CS) is an optimization algorithm developed by Xin-she Yang and Suash Deb in 2009.^[1][2] It was inspired by the obligate brood parasitism of some cuckoo species by laying their eggs in the nests of other host birds (of other species). Some host birds can engage direct conflict with the intruding cuckoos. For example, if a host bird discovers the eggs are not their own, it will either throw these alien eggs away or simply abandon its nest and build a new nest elsewhere. Some cuckoo species such as the New World brood-parasitic Tapera have evolved in such a way that female parasitic cuckoos are often very specialized in the mimicry in colors and pattern of the eggs of a few chosen host species ^[3]

Cuckoo search idealized such breeding behavior, and thus can be applied for various optimization problems. It seems that it can outperform other metaheuristic algorithms in applications.^[4]

Another seemingly unrelated algorithm for a completely different area of applications is called cuckoo hashing which was developed by Rasmus Pagh and Fleming Friche Rodler in 2001.^[5]

Contents 1 Cuckoo search 2 Random Walks and the Step Size 3 Implementation 4 Modified Cuckoo Search 5 Multiobjective Cuckoo Search (MOCS) 6 Hybridization 7 Applications 8 References

Cuckoo search

Cuckoo search (CS) uses the following representations:

Each egg in a nest represents a solution, and a cuckoo egg represents a new solution. The aim is to use the new and potentially better solutions (cuckoos) to replace a not-so-good solution in the nests. In the simplest form, each nest has one egg. The algorithm can be extended to more complicated cases in which each nest has multiple eggs representing a set of solutions.

CS is based on three idealized rules:

1. Each cuckoo lays one egg at a time, and dumps its egg in a randomly chosen nest;
2. The best nests with high quality of eggs will carry over to the next generation;
3. The number of available hosts nests is fixed, and the egg laid by a cuckoo is discovered by the host bird with a probability 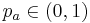. Discovering operate on some set of worst nests, and discovered solutions dumped from farther calculations.

In addition, Yang and Deb discovered that the random-walk style search is better performed by Lévy flights rather than simple random walk.

The pseudo-code can be summarized as:

Objective function: 
Generate an initial population of  host nests; 
While (t<MaxGeneration) or (stop criterion)
   Get a cuckoo randomly (say, i) and replace its solution by performing Lévy flights;
   Evaluate its quality/fitness 
         [For maximization,  ];
   Choose a nest among n (say, j) randomly;
   if (),
          Replace j by the new solution;
   end if
   A fraction () of the worse nests are abandoned and new ones are built;
   Keep the best solutions/nests;
   Rank the solutions/nests and find the current best;
   Pass the current best solutions to the next generation;
end while
Post-processing the results and visualization;

An important advantage of this algorithm is its simplicity. In fact, comparing with other population- or agent-based metaheuristic algorithms such as particle swarm optimization and harmony search, there is essentially only a single parameter 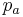in CS (apart from the population size ). Therefore, it is very easy to implement.

Random Walks and the Step Size

An important issue is the applications of Levy flights and random walks in the generic equation for generating new solutions

where 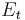is drawn from a standard normal distribution with zero mean and unity standard deviation for random walks, or drawn from Levy distribution for Levy flights. Obviously, the random walks can also be linked with the similarity between a cuckoo's egg and the host's egg which can be tricky in implementation. Here the step size determines how far a random walker can go for a fixed number of iterations. The generation of Levy step size is often tricky, and a good algorithm is Mantegna's algorithm.^[6]

If s is too large, then the new solution generated will be too far away from the old solution (or even jump out side of the bounds). Then, such a move is unlikely to be accepted. If s is too small, the change is too small to be significant, and consequently such search is not efficient. So a proper step size is important to maintain the search as efficient as possible.

As an example, for simple isotropic random walks, we know that the average distance traveled in the d-dimension space is

where 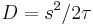is the effective diffusion coefficient. Here is the step size or distance traveled at each jump, and is the time taken for each jump. The above equation implies that^[7]

For a typical length scale L of a dimension of interest, the local search is typically limited in a region of 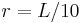. For 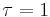and t=100 to 1000, we have 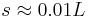for d=1, and 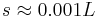for d=10. Therefore, we can use s/L=0.001 to 0.01 for most problems. Though the exact derivation may require detailed analysis of the behaviour of Levy flights.^[8]

Algorithm and convergence analysis will be fruitful, because there are many open problems related to metaheuristics^[9]

Implementation

The pseudo code was given in a sequential form, but Yang and Deb provides a vectorized implementation which is very efficient.^[10] In the real world, if a cuckoo's egg is very similar to a host's eggs, then this cuckoo's egg is less likely to be discovered, thus the fitness should be related to the difference in solutions. Therefore, it is a good idea to do a random walk in a biased way with some random step sizes. For Matlab implementation, this biased random walk can partly be achieved by

stepsize=rand*(nest(randperm(n),:)-nest(randperm(n),:));

new_nest=nest+stepsize.*K;

where K=rand(size(nest))>pa and pa is the discovery rate. A standard CS matlab can be found here [1]

An object-oriented software implementation of cuckoo search was provided by Bacanin^[11] On the other hand, a modified cuckoo search algorithm is also implemented for unconstrained optimization problems.^[12]

An open source implementation of Modified Cuckoo Search can be found here http://code.google.com/p/modified-cs/

Modified Cuckoo Search

A modification of the standard Cuckoo Search was made by Walton et al.^[13] with the aim to speed up convergence. The modification involves the additional step of information exchange between the top eggs. It was shown that Modified Cuckoo Search (MCS) outperforms the standard cuckoo search and other algorithms, in terms of convergence rates, when applied to a series of standard optimization benchmark objective functions.

Subsequently, the modified cuckoo search has been applied to optimize unstructured mesh which reduces computational cost significantly.^[14] In addition, another interesting improvement to cuckoo search is the so-called quantum-inspired cuckoo search with convincing results ^[15]

Multiobjective Cuckoo Search (MOCS)

A multiobjective cuckoo search (MOCS) method has been formulated to deal with multi-criteria optimization problems.^[16] This approach uses random weights to combine multiple objectives to a single objective. As the weights vary randomly, Pareto fronts can be found so the points can distributed diversely over the fronts.

Hybridization

Though cuckoo search is a swarm-intelligence-based algorithm, it can be still hybridized with other swarm-based algorithms such as PSO. For example, a hybrid CS-PSO algorithm seems to remedy the defect of PSO.^[17]

Applications

The applications of Cuckoo Search into engineering optimization problems have shown its promising efficiency. For example, for both spring design and welded beam design problems, CS obtained better solutions than existing solutions in literature. A promising discrete cuckoo search algorithm is recently proposed to solve nurse scheduling problem.^[18] An efficient computation approach based on cuckoo search has been proposed for data fusion in wireless sensor networks.^[19][20] A new quantum-inspired cuckoo search was developed to solve Knapsack problems, which shows its effectiveness.^[21]

A conceptual comparison of the cuckoo search with PSO, DE and ABC suggest that CS and DE algorithms provide more robust results than PSO and ABC.^[22] An extensive detailed study of various structural optimization problems suggests that cuckoo search obtains better results than other algorithms.^[23] In addition, a new software testing approach has been developed based on cuckoo search.^[24] In addition, cuckoo search is particularly suitable for large scale problems, as shown in a recent study.^[25] Cuckoo search has been applied to train neural networks with improved performance.^[26] Furthermore, CS is successfully applied to train spiking neural models.^[27] Cuckoo search has also been used to optimize web service composition process and planning graphs. ^[28]

Cuckoo search is a reliable approach for embedded system design^[29] and design optimization.^[30] An interesting application of cuckoo search is to solve boundary value problems.^[31]

References

Swarming Swarm algorithms Agent-based models Ant colony optimization Ant robotics Artificial Ants Bees algorithm Boids Crowd simulation Firefly algorithm Glowworm swarm optimization Particle swarm optimization Self-propelled particles Swarm intelligence Swarm (simulation) Biological swarming Agent-based model in biology Bait ball Collective animal behavior Feeding frenzy Flock Flocking Herd Herd behavior Mixed-species foraging flock Mobbing behavior Pack hunter Patterns of self-organization in ants Shoaling and schooling Sort sol Swarming behaviour Swarming (honey bee) Swarming motility Animal migration Animal migration Bird migration Bird migration flyways Diel vertical migration Fish migration Homing (biology) Insect migration Lessepsian migration Lepidoptera migration Reverse migration Salmon run Sardine run Sea turtle migration Tracking animal migration Swarm robotics I-Swarm Microbotics Swarm robotics Symbrion Related topics Allee effect Biomimicry Collective intelligence Eusociality Group size measures Microbial intelligence Mutualism Predator satiation Quorum sensing Spatial organization Stigmergy Swarming (military) Task allocation and partitioning of social insects

Optimization: Algorithms, methods, and heuristics   Unconstrained nonlinear: Methods calling ... ... functions Golden section search · Interpolation methods · Line search · Successive parabolic interpolation ... and gradients Convergence Trust region · Wolfe conditions Quasi–Newton BFGS and L-BFGS · DFP · Symmetric rank-one (SR1) Other methods Gauss–Newton · Gradient · Levenberg–Marquardt · Conjugate gradient ... and Hessians Newton's method   Constrained nonlinear General Barrier methods · Penalty methods Differentiable Augmented Lagrangian methods · Sequential quadratic programming · Successive linear programming   Convex minimization General Interior point method · Reduced gradient (Frank–Wolfe) · Subgradient method · Cutting-plane method Linear and quadratic Interior point Ellipsoid method of Khachiyan · Projective algorithm of Karmarkar · Semidefinite programming Basis-exchange Simplex algorithm of Dantzig · Criss-cross algorithm · Principal pivoting algorithm of Lemke   Combinatorial Paradigms Approximation algorithm · Dynamic programming · Greedy algorithm · Integer programming (Branch & bound or cut) Graph algorithms Minimum spanning tree Bellman–Ford algorithm · Borůvka · Dijkstra · Floyd–Warshall  · Johnson · Kruskal Network flows Dinic · Edmonds–Karp · Ford–Fulkerson · Push-relabel maximum flow   Metaheuristics Evolutionary algorithm · Hill climbing · Local search · Simulated annealing · Tabu search Categories (Algorithms · Methods · Heuristics) · Software